Cómo recubrir un plano o un volumen con varias redes de distribución o recolección
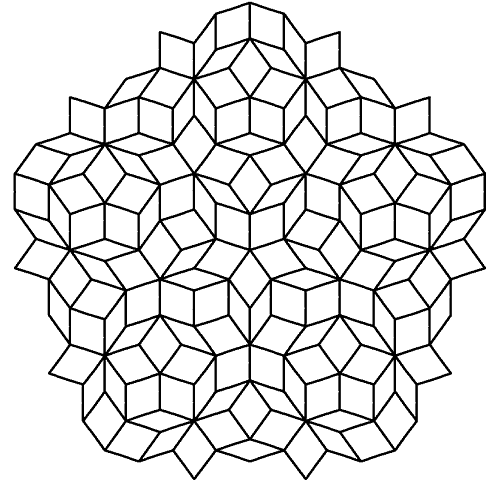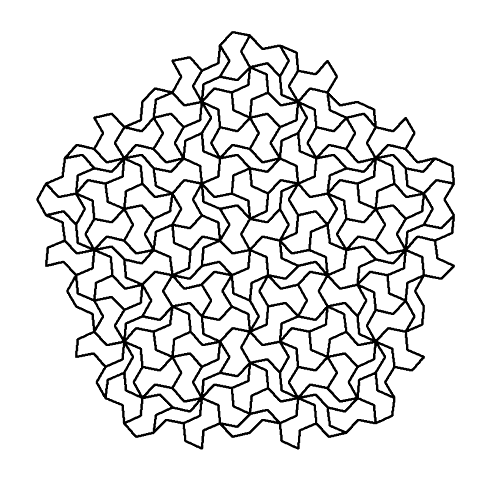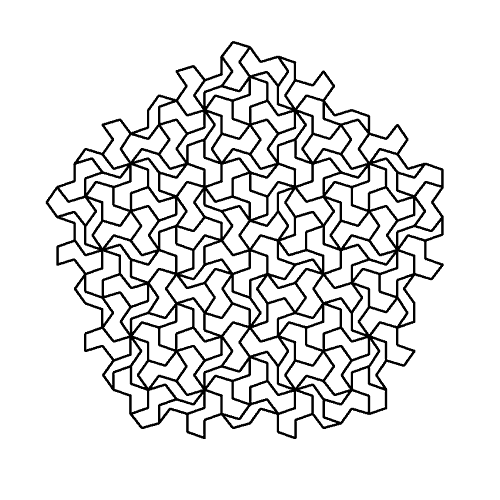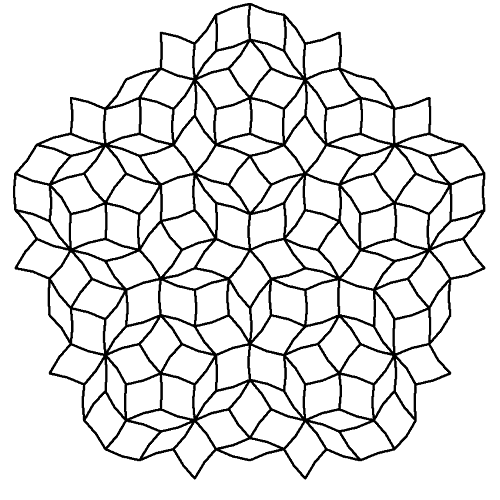
Cuando presenté el mapa de niveles de la ciudad flotante de Vikatee, el esquema del nivel 4 mostraba un curioso dibujo, que prometí explicar más adelante:
Los misteriosos Constructores de la ciudad buscaron la forma óptima para poder recoger o llevar líquidos o gases a los diferentes lugares, utilizando la mínima longitud posible de tuberías y por tanto ahorrando material y peso a la ciudad. Podemos imaginar el mismo problema en tres dimensiones si hubieran construido un habitáculo en el espacio (hmmm.. creo que utilizaré la idea en el próximo libro :-)
El caso es que los Constructores recurrieron a objetos ideados por dos venerables matemáticos de finales del siglo XIX y principios del XX: Georgi Voronoi y Waclaw Sierpinski, que había estudiado los trabajos del primero. De forma directa o indirecta, ambos trabajaron en el problema de cómo podía 'rellenarse' un plano.
Dividiendo el plano
Un problema que ha entretenido a los albañiles y matemáticos durante siglos es cómo dividir un espacio plano (un suelo, una pared, etc.) en trozos que lo recubran sin dejar huecos y sin intersectarse. Es lo que los matemáticos llaman técnicamente una partición. Cuando esta partición se consigue reutilizando elementos geométricos similares (losas, baldosas o teselas, 'tiles' en inglés) se llama teselación. Os recomiendo esta página donde se muestran las diferentes técnicas.
Todos estamos familiarizados con los teselados regulares o semiregulares, que repiten elementos de la misma forma (o formas) periódicamente. Encontramos estas teselaciones en cualquier casa y como decoración en suelos, paredes y techos.
Los maestros de la teselación decorativa fueron sin duda los artistas musulmanes, como podemos comprobar en la Alhambra y otros monumentos:
El genial artista holandés M.C. Escher se basó en estas teselaciones para construir las suyas con animales, ángeles o demonios:
En todos los ejemplos anteriores encontramos periodicidad, la repetición de un patrón determinado. Sin embargo, existen teselaciones aperiódicas que aún siendo regulares (los elementos se repiten), no son periódicas, no existe un patrón. Con ellas puede rellenarse un plano infinito sin que tengamos necesidad de repetirnos.
Fue necesario el trabajo de un matemático de la talla de Roger Penrose en los años 70 para demostrar que podían construirse teselaciones aperiódicas con solamente dos tipos de baldosas:
El problema que abordó Voronoi fue diferente: si tenemos una serie de puntos P esparcidos por un plano, ¿cómo se dividiría el plano en regiones, de tal forma que dentro de una región R estamos más cerca de un punto pR que de cualquier otro? Lo podéis ver en esta imagen:
Estos 'diagramas de Voronoi' pueden construirse igualmente para puntos en el espacio 3D o de más dimensiones. Una mina para arquitectos visionarios:
Por tanto, si un fontanero espacial se planteara cómo construir una red de canalizaciones en una ciudad voladora plana o en 3D (imaginad una explotación minera de un asteroide), podría dividir todo ese espacio en regiones que serían las más cercanas a los puntos donde se localizaran las centrales de distribución o recolección, ahorrando así tiempo y recursos.
Aprovechando que tenemos a mano a M.C.Escher:
¿Se puede rellenar el plano con una línea?
Suponiendo que hemos dividido nuestra ciudad en varias regiones utilizando la técnica de Voronoi, ¿cómo crearíamos la red de distribución más eficiente en cada región, a partir del punto central? Tendremos en cuenta que en cualquier lugar puede producir o necesitar la misma cantidad de fluido.
Para responder a esta pregunta podemos apoyarnos en otro problema en el que trabajaron los matemáticos del siglo XIX: ¿puede rellenarse un plano con una línea? A priori parecería que ésta es una tarea imposible, teniendo en cuenta que una línea matemática es infinitamente delgada, y el plano contiene un número infinito de puntos.
Sin embargo, Georg Cantor había demostrado que el infinito de puntos en el plano era equivalente al de puntos de una línea (no hay en realidad 'más puntos' en el plano que en la línea), y por lo tanto debía ser posible establecer una correspondencia entre puntos de una línea y los de un plano. Dicho de otra manera, debería ser posible representar los puntos de un plano con una sola coordenada en lugar de dos coordenadas.
Así, los grandes matemáticos de la época construyeron unas curvas por sucesivas iteraciones, de manera que al repetirse éstas infinitas veces se conseguiría rellenar todo el plano. Podemos ver a continuación cómo se construían estas curvas:
Peano
Hilbert
Moore
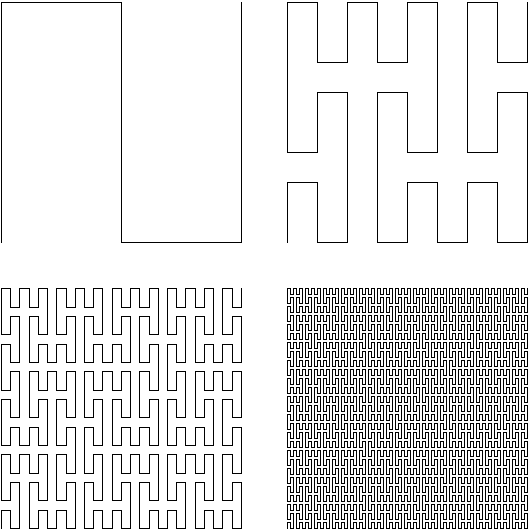
Y aquí entra nuestro segundo fontanero honorario, Sierpinski, pues en la construcción de su curva cerrada se va generando una ramificación progresiva desde un punto central, y si nos fijamos existen puntos terminales de esta ramificación que llegan a todos los puntos del plano con una distancia mínima desde el punto central (no en línea recta, pero sí teniendo en cuenta la restricción de ángulos rectos).
Sierpinski
En realidad, Sierpinski se hizo más famoso por otro tipo de construcción, en el que el espacio no se rellena completamente, sino dejando huecos. Este tipo de objeto geométrico se llama un fractal, y se caracteriza por su autosimilaridad y por tener una dimensión fraccional. Por ejemplo, una alfombra de Sierpinski tiene una dimensión 1.58, entre 1 y 2.
Existen infinidad de variaciones sobre este tema, más o menos románticas:
Fontanería de Vikatee
Pero volviendo a nuestro problema original, vemos ahora que la idea de Voronoi, dividir el espacio en regiones de 'cercanía' a un conjunto de puntos, se puede combinar con la idea de Sierpinski de un árbol que llega con distancias mínimas a todos los puntos de una región.
Podéis comprobar ahora cómo el plano del nivel prohibido de Vikatee se construyó dividiendo el rectángulo de la ciudad en regiones cercanas a una serie de puntos, y trazando árboles similares a los de Sierpinksi a partir de éstos. En realidad me salté las reglas de ambos (Voronoi y Sierpinski) cuando me convino, pero la inspiración está ahí, ja ,ja.
Así que ya lo sabéis, para cuando diseñéis vuestras futuras construcciones espaciales, hay matemáticos que han pensado en todo :-)
Hasta la próxima,
Salvador