Fractales: la geometría infinita

¿Cómo surge la complejidad a partir de lo simple? ¿Por qué vemos las mismas estructuras repetidas por doquier en la naturaleza? Para responder a estas preguntas tenemos que recurrir a unos objetos geométricos que son a la vez extraños y omnipresentes, los fractales.

Como prueba de su omnipresencia, en el blog hemos visto ya los fractales en acción en varias entradas: al hablar de universos anidados en la mitología hindú, curvas capaces de rellenar un plano, la dinámica de conflictos entre los personajes de una historia, la estructura narrativa, la densidad de materia en el espacio y ejemplos de animaciones psicodélicas.

Históricamente, el primer objeto matemático con características fractales fue definido por el matemático Karl Weierstrass en 1872. Pero los fractales no se popularizaron y trataron rigurosamente hasta el trabajo del matemático Benoit Mandelbrot en los años 1970, ayudado por los ordenadores como instrumento de cálculo e investigación.

 

Hoy en día las técnicas fractales son ubicuas en campos como los sistemas dinámicos no lineales (caos), los efectos especiales, la compresión de datos, modelos del mercado bursátil, análisis y generación automática de música, etc.

¿Qué es un fractal?

Un fractal es un objeto que puede 'vivir' en un espacio de 1, 2, 3 o cualquier número de dimensiones, y que se caracteriza por:

• Ser autosimilar: la forma de la totalidad de un fractal es igual o muy similar a la de sus partes. Aquí podéis verlo en un extracto del documental que encontraréis completo al final:

Podemos ver aquí otro ejemplo de autosimilaridad en la función de Weierstrass, el primer objeto fractal que fue definido:

Y otro ejemplo más, bastante tenebroso:

• Como consecuencia de la autosimilitud, el fractal es aproximadamente igual en cualquier escala de detalle.

Por ejemplo, al observar una fotografía de un terreno natural como la siguiente resulta prácticamente imposible saber cuál es su escala de tamaño: ¿10 metros, 100 metros, 1000 metros...?

... hasta que no tenemos como referencia otros objetos de tamaño conocido:

En las películas antiguas se utilizaba frecuentemente esta característica para crear efectos especiales en los que las maquetas o monstruos aparecían mucho más grandes de lo que eran en realidad.

• En un fractal definido matemáticamente, la autosimilitud se aplica a todas las escalas de detalle, lo cual implica que el fractal tiene detalles infinitamente pequeños. Aunque escojamos una parte muy pequeña, esa parte es igual de compleja que el todo. Esta propiedad se ha explotado visualmente para hacer increíbles animaciones en las que nos 'zambullimos' en escalas cada vez más y más pequeñas dentro del fractal, donde podemos encontrarnos de nuevo con el objeto del que partimos:

• El trabajo original de Weierstrass se originó en la necesidad de demostrar que era posible tener una curva continua (sin roturas) pero que no sea suave en ningún punto. El concepto matemático se denomina no diferenciabilidad. En términos sencillos, significa que cualquier punto que escojamos en un fractal es un 'pico': no podemos definir la línea tangente, porque no hay ni una sola zona suave donde medirla.

Esta propiedad de no-diferenciabilidad se relaciona con otras extrañas características de los fractales: la imposibilidad de calcular medidas como valores medios, longitudes y áreas. Dependiendo de la escala de detalle que utilicemos para realizar estas medidas obtendremos un valor u otro, y éste irá variando también como un fractal. De hecho el artículo original de Mandelbrot sobre los fractales se llamó "¿Cuán larga es la costa de Gran Bretaña?". En él demostró que la medida de longitud no tenía sentido para un fractal. La longitud de la costa de Gran Bretaña se va haciendo más y más grande a medida que la vemos a mayor detalle.

En lugar de las medidas habituales, para los fractales utilizamos la dimensión fractal. Su definición matemática no es trivial, pero el significado tiene que ver con qué parte del espacio en el que vive puede rellenar el objeto fractal.

Así, un objeto fractal que vive 'dentro' de una línea (las líneas tienen dimensión 1), tendrá una dimensión fractal entre 0 y 1. Cuando más rellene la línea, más cerca estará de la dimensión 1.

Los fractales que viven en un plano (2 dimensiones) tendrán una dimensión fractal entre 1 y 2 (como en la figura anterior), y así sucesivamente para cualquier número de dimensiones.

En esta página podéis ver muchos objetos fractales clasificados por el valor de su dimensión.

Fractales que viven en una línea

En 1883, poco después del trabajo de Weierstrass, Georg Cantor, que estudiaba las propiedades de conjuntos infinitos, demostró algo curioso: definió un conjunto de puntos contenido en un segmento de línea de longitud 1, cuya medida era nula (puestos todos los puntos juntos su longitud era cero, no rellenaban ningún espacio en la línea en sentido clásico), y sin embargo el número de puntos en este conjunto de Cantor era infinito e igual al número de puntos que formaban todo el segmento.

Este conjunto, también llamado 'polvo de Cantor', puede formarse eliminando sucesivamente (hasta el infinito) el tercio central del segmento de línea y de los segmentos que resultan:

La dimensión de este conjunto es menor que uno, concretamente Log(2)/Log(3)=0.631.

El conjunto de Cantor muestra claramente que un fractal puede ser un conjunto disconexo de puntos, aunque otros muchos fractales sí son conexos y continuos, como los que veremos a continuación.

Fractales en el plano

Ya hemos visto que la función de Weierstrass forma una curva fractal en el plano. En 1904, Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch.

En este caso la curva se forma añadiendo recursivamente triángulos cada vez más pequeños sobre los lados de la curva de nivel anterior:  

Nos encontramos de nuevo con un objeto autosimilar, igual en todas las escalas y con picos en cada uno de los puntos de la curva:

La dimensión fractal de la curva de Koch es log 4/log 3 ≈ 1.26186. 

Curiosamente, si utilizamos copos de Koch de dos tamaños podemos cubrir el plano sin huecos. Sus bordes infinitamente detallados encajan perfectamente:

Como vimos en esta entrada, existen otras muchas curvas de tipo fractal (Peano, Hilbert, Moore, Sierpinksi) que rellenan el plano de forma sistemática (todos los puntos del plano pertenecen a la curva), y por tanto tienen una dimensión fractal igual a 2.

En 1915, Waclaw Sierpinski construyó su triángulo y un año después su alfombra:

A pesar de que estas figuras parecen tener área, son conjuntos de medida nula: en el límite infinito no rellenan ninguna parte del plano en el sentido convencional. Sin embargo, podemos definir su dimensión fractal. La dimensión del triángulo es:

Y la de la alfombra, que intuitivamente parece 'cubrir más área', es 1,892789...

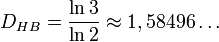
Rellenando el espacio

Es fácil extender a 3 dimensiones muchos de los objetos que hemos visto antes. Por ejemplo, si vamos eliminando los tercios que bisectan cada cara de un cubo podemos generar un conjunto de Cantor tridimensional:

También podemos construir con un tetraedro una figura 3D similar al triángulo de Sierpinski: 

O utilizan un cubo, en lugar de un cuadrado, para construir una alfombra de Sierpinski en 3D:

Hay sistemas sencillos de generación de fractales que pueden dar resultados espectaculares en 3D. Por ejemplo, el programa Mandelbulb es un sistema de visualización y animación 3D especialmente pensado para fractales.

Aquí tenemos un ejemplo digno de M.C. Escher:

Fractales iterativos en el campo complejo: Julia y Mandelbrot

Viendo los anteriores ejemplos de fractales definidos por fórmulas matemáticas, podríamos pensar que con unas reglas de construcción sencillas obtenemos siempre estructuras repetitivas y simples.

Sin embargo el mundo de los fractales dio una gran sorpresa a través del trabajo de Mandelbrot y otros que tuvieron acceso a ordenadores para ejecutar cálculos repetitivos de forma rápida. En particular, a partir del estudio del comportamiento de los polinomios de variable compleja, se descubrió que la iteración de una expresión como...

(siendo Zi un número complejo = x + y.i, que se puede representar en un plano con su parte real x e imaginaria y)

... tenía un comportamiento muy extraño cuando la iteración se repetía un número grande de veces. El valor de Zn se podía hacer muy grande, o bien quedarse pequeño. Al dibujar en el plano los puntos Z que tras muchas iteraciones seguían siendo pequeños (cercanos al centro) apareció una figura (el conjunto de Mandelbrot) cuya complejidad resultaba asombrosa.

Mandelbrot demostró que este conjunto cumplía todas las características de un fractal, pero a pesar de estar definido por una fórmula tan sencilla y de su carácter autosimilar, la variedad de estructuras que se encontraban en su interior era infinita y eternamente fascinante, como un zoo matemático sin fin, lleno de una multitud inagotable de criaturas siempre nuevas.

El número de imagenes y animaciones del conjunto de Mandelbrot es incontable, y existen paquetes de software que permiten explorarlo por cuenta propia. Os pongo aquí solamente una pequeña muestra:

Esta animación representa uno de los zooms más profundos hacia el interior del conjunto realizados hasta la actualidad. Como vemos, nos encontramos en varias ocasiones con versiones más pequeñas del mismo conjunto, lo que demuestra su autosimilaridad:

La idea del conjunto de Mandelbrot se generalizó rápidamente para un conjunto de funciones complejas que dan lugar a los llamados conjuntos de Julia, pudiendo pasarse de un conjunto a otro sin más que cambiar unos pocos valores numéricos.

En este didáctico video podéis ver la explicación del proceso de cálculo de los conjuntos de Julia en forma gráfica:

También es posible generalizar a 3D las fórmulas de los conjuntos de Julia para obtener una visión tridimensional:

Aquí tenéis otro de esos videos de zoom casi infinito, esta vez de un conjunto de Julia:

Más allá del 3D

Como hemos comentado, podemos crear fractales con cualquier número de dimensiones. Una opción para tener más de tres dimensiones es utilizar el tiempo, introduciendo cambios en los fractales. Estos videos han sido generados con el programa Mandelbulb comentado antes, y utilizan este efecto de cambio temporal:

A la inversa, si creamos un fractal en cuatro dimensiones y hacemos un 'corte' en 3D que se mueva a su través, lo que vemos es un fractal que parece animarse con el tiempo:

Esta técnica se usa, por ejemplo, para generar nubes fractales animadas. Aquí vemos el mismo método aplicado al conjunto de Mandelbrot, mostrando una especie de 'fantasma' 3D del conjunto en cuatro dimensiones:

Obviamente es posible generar fractales de dimensiones aún más grandes, pero resultaría muy difícil visualizarlos.

Fractales de similaridad no exacta

Hasta ahora hemos hablado de fractales generados a partir de fórmulas matemáticas o construcciones geométricas. Sin embargo, los procesos de la naturaleza, las leyes de la física, la biología o el mercado de valores pueden crear también estructuras fractales, debido a su naturaleza de sistemas no lineales con tendencias opuestas de contracción y expansión.

En estos fractales naturales la autosimilitud no es exacta, sino en promedio. Se sigue dando el fenómeno de la indistinguibilidad de escalas como que en los fractales matemáticos, aunque los patrones no se repiten de forma exacta en los diferentes niveles de detalle.

Otra característica de los fractales naturales es que la dimensión fractal no permanece constante en todas las escalas. Por ejemplo, un terreno natural puede tener una dimensión más 'rugosa' en una escala de detalle (más salientes debidos a las rocas y piedras individuales) y dimensión más 'suave' a gran escala, debido a efectos de la erosión. Este hecho se utiliza al generar terrenos sintéticos para efectos especiales.

En este video del programa Redes vemos con claridad varios ejemplos de cómo la naturaleza utiliza las formas fractales:

Y en este otro episodio de Redes, el incombustible Punset entrevista al 'creador' mismo, Monsieur Mandelbrot, acerca de la relación de los fractales con la naturaleza y el arte:

En particular, algunos fractales naturales, como las formas en espiral de galaxias y flores, se producen como consecuencia de la autosimilitud de la razón áurea. Se trata de los llamados fractales de Fibonacci:

Un terreno insospechado donde aparecen las formas fractales es en la evolución de los mercados de bolsa, y en particular en los valores de la acciones y los índices bursátiles. Por ejemplo, si uno observa estas gráficas resulta imposible saber cuál es su escala de tiempo. La evolución del mercado en una semana es similar (con el factor de escala correspondiente) a la evolución en un año o en diez años, aunque obviamente la autosimilitud es solo estadística (si fuera exacta sería muy fácil predecir la bolsa).

La razón de la naturaleza fractal de los valores es la dinámica no lineal que subyace a los mercados por las dos tendencias opuestas que los dominan: vender (baja los valores) y comprar (los sube). Sin embargo, el consenso es que precisamente por la naturaleza caótica de estos sistemas, la estructura fractal no es de mucha ayuda para realizar predicciones.

Un área donde la aplicación de los fractales ha sido muy fructífera es en el análisis de estructuras en música y en plástica. Por ejemplo, se pueden caracterizar diferentes autores o estilos, incluso épocas del mismo autor, por el uso de diferentes dimensiones fractales.

Se especula también sobre en qué medida la dimensión fractal y sus variaciones tienen influencia en nuestra percepción de la belleza en objetos naturales y artísticos. Lo que es cierto sin duda es que nuestro cerebro identifica y responde a esta información.

Además de usarse para generar imágenes, la teoría fractal se utiliza cada vez más para generar música de forma automática, con características similares a la compuesta por humanos. Un ejemplo es el programa FracMus, desarrollado por un pianista y compositor español, Gustavo Díaz-Jerez. Otro ejemplo es el software Tune Smithy.

Aquí tenéis un par de ejemplos de música fractal:

La estructura fractal de la música sirve también de inspiración a un grupo del MIT para crear nuevos materiales con sorprendentes propiedades.

Métodos de generación

¿Cómo podemos generar un objeto fractal? Una idea es recrear su compleja forma a partir de unas reglas sencillas de autosimilaridad, lo que podemos conseguir de varias formas:

• Construcción recursiva: un fractal de nivel N se dibuja o construye con los de nivel N-1, y así hasta llegar a un nivel básico que es la forma elemental. Esta es la forma en que se construyen curvas como la de Koch, Peano, etc., y figuras como las de Sierpinksi. A continuación tenemos un ejemplo un poco más complicado: la curva dragón (llamada así por que parece dibujar la forma de un dragón):

• Una técnica para formalizar este tipo de construcción recursiva utiliza las llamadas gramáticas formales, que indican cómo un símbolo se sustituye por otros, lo cual se puede hacer de manera repetida. Un ejemplo particularmente útil son los L-sistemas, utilizados para representar procesos de crecimiento natural como los de ramificación de árboles y plantas. Variando las reglas gramaticales y diversos parámetros numéricos que aparecen en ellas, se pueden crear una gran variedad de estructuras de aspecto natural:

Los L-sistemas no solo pueden utilizarse para crear estructuras geométricas, sino también sonidos, como en este ejemplo:

• Otra forma de generación relacionada con la autosimilaridad es el método basado en Sistemas Iterativos de Funciones. La idea es construir varias tranformaciones geométricas, cada una de las cuales representa una correspondencia o autosimilaridad en el fractal, y luego aplicar de forma iterada y sucesiva estas funciones de transformación a un punto. El resultado es que, aunque parezca sorprendente, las sucesivas posiciones del punto van dibujando el fractal completo.

Por ejemplo, el conjunto de Cantor puede generarse utilizando las dos funciones 

  y

para valores de x entre 0 y 1.

El ejemplo más clásico de este sistema de generación es el helecho de Barnsley. En este caso se utilizan tres funciones de autosimilaridad, una para la parte superior y otras dos para las partes inferiores derecha e izquierda, cada una de ellas igual al helecho completo:

Aquí podéis ver cómo se va formando la figura añadiendo sucesivos puntos en los lugares dados por una de las funciones de transformación del sistema, escogida aleatoriamente entre las tres.

Hay otros sistemas de generación de fractales que no se basan en reproducir la autosimilaridad. Por ejemplo, hemos visto los sistemas de iteración de funciones complejas para los conjuntos de Mandelbrot y Julia, en los que se comprueba el tiempo de escape para determinar si un punto pertenece o no al conjunto. Este tiempo se escape se utiliza para asignar los diferentes colores que vemos en las imágenes y vídeos.

Para los fractales de similaridad estadística hay que utilizar métodos que incluyan un elemento de azar, pero cuya variación resulte definida según la escala.

Para ciertas estructuras que se forman en la naturaleza por agregación de partículas (caso de los copos de nieve, por ejemplo) se reproduce por ordenador este proceso de agregación sucesivo.

Para los fractales definidos como una función de altura sobre una o más variables (por ejemplo, una curva de una función y=f(x), o una superficie de un terreno o del agua: z=f(x,y) ) podemos utilizar un método de subdivisión, como se ve estupendamente en el siguiente video, en el que se pega también una textura fractal sobre el terreno para conseguir un mayor realismo.

Con el mismo propósito podemos utilizar también el método de superposición de ondas, bien mediante el método de síntesis de Fourier (ondas sinusoidales) o con ondículas (wavelets). Si sumamos ondas de frecuencia cada vez mayor, disminuyendo al mismo tiempo su amplitud, conseguimos una superficie que es estadísticamente autosemejante.

Este método se usa con gran realismo para simular el oleaje en el mar:

Aquí tenemos una sencilla aplicación basada en ondículas para generar un terreno fractal:

Para terminar con los fractales, este magnífico documental sirve como resumen de todo lo que hemos tratado:

Fractales y seudociencia

Por desgracia, al igual que sucede con el término 'cuántico', en muchas ocasiones hay una apropiación del término 'fractal' para dar un aire serio a ideas pseudocientíficas.

Pongo aquí algunos ejemplos que he encontrado mientras buscaba información. Ojo avizor.

• ¿Estructura fractal de la Biblia?

• 'Ciencia fractal' y alimentación cuántica' (!?)

• Otro pupurri pseudocientífico que mezcla lo 'cuántico' y los 'fractales'

• Curación con fractales

• Pseudofractales para inversionistas incautos

Pues hasta la próxima. Tengan cuidado ahí fuera  ;-)

   Salvador