Un número irracional y recursivo
En Matemáticas existen diferentes tipos de números. Todos conocemos los enteros y los fraccionarios (el cociente de dos enteros). También usamos los números reales (corresponden a la longitud de un segmento de recta o a una distancia). No todos los reales son fraccionarios, se trata de los números irracionales, que no se pueden calcular como un cociente de enteros.
A su vez, hay dos tipos de números irracionales: los algebraicos no racionales y los trascendentes. Los números algebraicos son todos los que se pueden calcular como solución de ecuaciones polinómicas: incluyen a las raíces cuadradas, cúbicas... y sus combinaciones (pero no a las series infinitas de éstos), así como a otros números que no pueden expresarse mediante raíces.
Un tipo de números algebraicos son los construíbles, que representan la longitud de un segmento que se puede definir mediante regla y compás, y que es una combinación de operaciones de suma, resta, multiplicación, división y raíces cuadradas sobre enteros.
Por ejemplo, el número phi (φ o Φ), llamado razón áurea o número áureo, resulta ser un número algebraico construíble que es la solución a la siguiente ecuación polinómica:
De donde podemos obtener el valor de phi:
Veremos cómo es construible, ya que desde la antigüedad se conocían diferentes métodos para generarlo mediante regla y compás.
Por otra parte hay números irracionales que no son algebraicos (no son solución de ecuaciones polinómicas) y que se denominan trascendentes. No existen muchos números de los cuales se haya conseguido demostrar que son trascendentes, y por ello les rodea una cierta aura mística. De hecho algunos, como la constante de Euler, ni siquiera se sabe con seguridad si son racionales o trascendentes.
Los ejemplos más conocidos de números trascendentes son los números π y e, y los valores de los logaritmos naturales (de base e).
Los ejemplos más conocidos de números trascendentes son los números π y e, y los valores de los logaritmos naturales (de base e).
Interpretación geométrica y numérica
Como su nombre indica, la razón áurea phi es un cociente entre dos números. Se puede interpretar geométricamente como la relación entre dos segmentos rectos (a y b) tal que la longitud del segmento largo (a) dividido por el corto (b) es también igual al cociente entre la suma de los dos (a + b) dividida por el segmento largo (a), tal como expresa la siguiente figura.
De esta última igualdad resultan las ecuaciones 1 anteriores que nos permiten calcular el valor de phi.
Una forma muy frecuente en la que aparece la razón áurea es en el llamado rectángulo áureo, que tiene una base igual a la suma de los segmentos a + b y una altura igual al segmento largo a.
Este rectángulo se puede construir con regla y compás como se muestra en la siguiente figura:
La razón áurea presenta interesantes propiedades de autosimilaridad y recursividad. Por ejemplo, si en la figura anterior quitamos el cuadrado de la izquierda (de lado a) nos queda un rectángulo vertical más pequeño que es también un rectángulo áureo, y este proceso puede ser repetido indefinidamente, creando una espiral de rectángulos áureos cada vez más pequeños, como muestran las siguientes animaciones.
Podemos llegar al mismo resultado espiral de otra manera, pues la razón áurea también tiene una interpretación numérica asociada a la sucesión de Fibonacci. Esta sucesión de números se define como aquella en la que cada número es igual a la suma de los dos anteriores. Normalmente se escogen el 0 y el 1 (o dos unos) como los primeros números y a partir de ellos se calculan los demás:
Si calculamos ahora el cociente entre cada número de Fibonacci y el anterior, veremos que este valor se acerca cada vez más a la razón áurea, pudiéndose demostrar que en el límite infinito es exactamente igual a phi.
La presencia de la razón áurea en diferentes ramas de la matemática no termina aquí. ¿Recordáis el problema de la teselación o división del plano? Todos sabemos recubrir fácilmente el plano con triángulos regulares (3 lados), cuadrados (4 lados) o hexágonos regulares (6 lados). ¿Pero qué pasa con los pentágonos (5 lados)? A diferencia de los demás polígonos regulares sencillos, no podemos utilizarlos para recubrir el plano sin dejar huecos:
Como se explica aquí, la solución de esta paradoja la resolvió el matemático Roger Penrose, dándose cuenta de que las partes de un pentágono regular pueden organizarse en dos losetas o teselas diferentes, que sí pueden recubrir el plano. Lo curioso es que no lo recubren de una forma periódica como los polígonos regulares, sino de una manera en la que nunca se repite el mismo patrón.
Las dimensiones de las losetas de Penrose siguen la proporción geométrica de la razón áurea. Esto era previsible, al ser partes de un pentágono. Pero lo más alucinante es que si calculamos la proporción entre el número de veces que se utiliza una tesela y la otra al rellenar el plano con ellas, esta proporción también es igual a la razón áurea.
La belleza clásica
Además de su intrínseca belleza matemática, los artistas pronto se dieron cuenta de que había algo especialmente armonioso en la razón áurea, bien como proporción entre longitudes, o bien en la forma del rectángulo áureo. Así, en la historia del arte se encuentran innumerables ejemplos del uso premeditado de esta proporción en arquitectura, pintura y diseño.
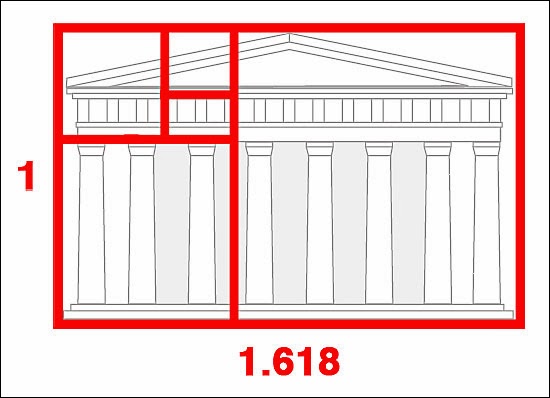
Uno de los casos más citados es el de las proporciones del Templo de Atenea en la acrópolis de Atenas, el Partenón. De hecho, el nombre phi para la razón áurea proviene de Phidias (Fidias), el arquitecto que coordinó toda la obra y ejecutó las esculturas que la acompañaban.
La razón áurea se utilizó una y otra vez para establecer todas las proporciones entre las diferentes partes de este monumento, como se puede apreciar en las siguientes figuras.
Si se ponen en relación todas estas proporciones en el diseño de la fachada, se puede construir una espiral de Fibonacci:
Los rectángulos y proporciones áureas se utilizan también en la planta del templo:
El uso de la razón áurea no se limita a los antiguos. Por ejemplo, las diferentes secciones de la Torre Eiffel fueron diseñadas para que su altura estuviera en proporciones mutuas iguales a la razón áurea, como se observa en estas figuras.
Tampoco el uso de la razón áurea se limita a la arquitectura. Leonardo da Vinci, que era un 'friki' de las proporciones, utilizó la razón áurea para definir las relaciones entre los elementos de sus obras, como la Mona Lisa. Veremos en la siguiente sección que tenía buenas razones para hacerlo.
En este fantástico blog sobre geometría y arte podéis encontrar muchos ejemplos más.
Hoy en día, se sigue utilizando la razón áurea en el diseño de muchos objetos:
Incluso en algunos diseños tan prosaicos como un carnet de identidad:
Incluso los Constructores de la ciudad flotante de Vikatee (en mi libro "La Ciudad de las Esferas") utilizaron la razón áurea para establecer sus proporciones :-)
La belleza natural
Además de por su belleza matemática, su carácter misterioso como número irracional y la aparente armonía que otorgaba, los artistas clásicos utilizaron la razón áurea tras comprobar que aparecía en numerosos 'diseños' de la naturaleza, comenzando por las proporciones del cuerpo humano. Esto les llevaba a pensar (y aún hay personas que opinan así) que la razón áurea era algo así como un canon divino implantado en el universo. Hoy sabemos que la llamada 'proporción divina' tiene en realidad que ver con los procesos de crecimiento y optimización de las formas.
Hay bastantes ejemplos de la presencia en la naturaleza de las espirales de Fibonacci. Muchos de estos ejemplos provienen del mundo de las plantas, de la forma en que se disponen sus ramificaciones, pétalos, semillas y otros elementos:
Pero también aparecen espirales de Fibonacci en el mundo animal, como en las conchas de los moluscos:
En este vídeo podemos ver animaciones creadas mediante impresión 3D con estructuras de Fibonacci:
Más asombrosa aún es la presencia de la espiral dorada en fenómenos de escalas tan diferentes como los ciclones y huracanes o las galaxias espirales:
La razón de que estas espirales aparezcan en las plantas es que en el proceso de crecimiento, la distribución de los elementos (pétalos, semillas, etc.) se optimiza para recibir mayor luz solar u ocupar más superficie. Esta situación óptima se produce cuando están separados por el ángulo áureo, también relacionado con la razón dorada. Podéis consultar este artículo o éste sobre las espirales en las plantas, o ver el siguiente video:
Incluso la espiral que gobierna nuestra herencia genética, el ADN, sigue de manera bastante aproximada la proporción áurea, tanto en la separación entre las dos hélices como en la proporción entre anchura y altura de la vuelta de cada hélice.
Otra aparición misteriosa de la razón áurea en la naturaleza se registra en las proporciones de los cuerpos animales, entre ellos el cuerpo humano.
Los elementos que forman las extremidades están en proporción sucesivamente más pequeña, desde la falange más extrema, pasando por la extensión de la mano respecto al antebrazo, y del antebrazo respecto al brazo, siempre siguiendo la razón áurea. No he encontrado ninguna razón que explique por qué esto es así (si alguien la encuentra, que me la envíe). Mi corazonada es que tiene que ver con la optimización del movimiento de las extremidades, utilizando una menor energía con un máximo alcance en distancia.
Recientemente se ha comprobado también que los rostros identificados como más perfectos o bellos tienen sus proporciones ajustadas a la razón áurea, incluyendo las orejas y la dentadura. No os perdáis este alucinante video:
Pero, ¿por qué percibimos la proporción áurea como más bella o armoniosa? La explicación seguramente tiene que ver con que evolutivamente hemos aprendido a detectar la proporción áurea como más deseable, propia de las plantas o animales más sanos, más 'optimizados'.
Con todo este bagaje no os extrañará que mi escritor de ciencia-ficción favorito, Philip K. Dick, tuvo entre sus visiones una en la que aparecía una puerta a otra dimensión con la forma de un rectángulo áureo.
Hasta la próxima,
Salvador


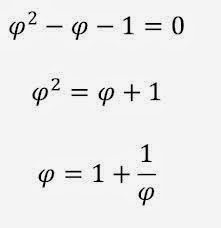

































Por cortesía de Xavier Cabrera, podéis ver aquí unas fotografías alucinantes de una espiral de plancton formada en el océano: http://earthobservatory.nasa.gov/IOTD/view.php?id=82761 Notad que, sin embargo, no todas las espirales son de tipo áureo o logarítmico, sino que hay otros tipos dependiendo de cómo se van alejando del centro (http://es.wikipedia.org/wiki/Espiral#Espirales_bidimensionales).
ResponderEliminarDejo aquí también un enlace a un MARAVILLOSO VIDEO sobre las espirales de Fibonacci, con alucinantes animaciones: http://www.wimp.com/fibonaccisequence/
ResponderEliminar